Bihar Board Class 8 Maths Solutions Chapter 9 बीजीय व्यंजक

Bihar Board Class 8 Maths Solutions Chapter 9 बीजीय व्यंजक Text Book Questions and Answers.

Bihar Board Class 8 Maths Solutions In Hindi Chapter 9 बीजीय व्यंजक

Bihar Board Class 8 Maths Solution In Hindi बीजीय व्यंजक Ex 9.1

बीजीय व्यंजक Class 8 Bihar Board प्रश्न 1.
जोडिए-

a) xy , 3xy
(b) x² + 3x , 2x + 9
(c) x², y²
(d) 7x , –8x
(e) 8a , -2a , 7a , 2b
(f) 8x , -2x , -6x
(g) 2.3x , 1.7x
(h) 2/3x , 1/3x , -x

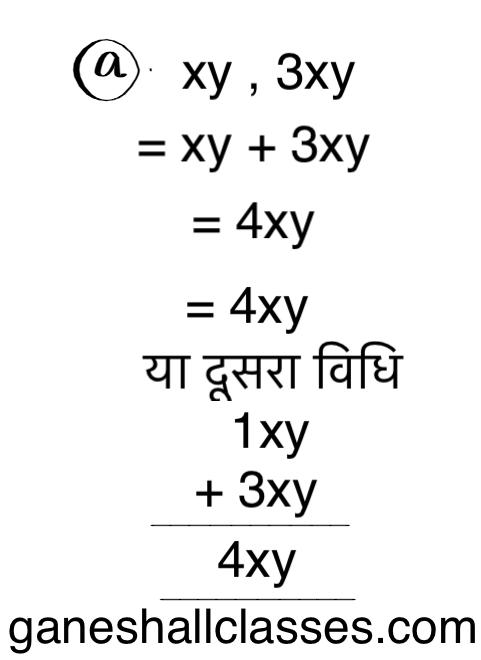
(b). x² + 3x , 2x + 9
= x² + 3x + 2x + 9
= x² + 5x + 9
(c). x² , y²
= x² + y²
(d). 7x , -8x
= 7x + (-8x)
= 7x – 8x
= – x
(e). 8a , -2a , 7a , 2b
= 8a + (-2a) + 7a + 2b
= 8a – 2a + 7a +2b
= 15a – 2a + 2b
= 13a + 2b

(f). 8x , -2x , -6x
= 8x + (-2x) + (-6x)
= 8x – 2x – 6x
= 6x – 6x
= 0
(g). 2.3x , 17x
= 2.3x + 1.7x
= 4x

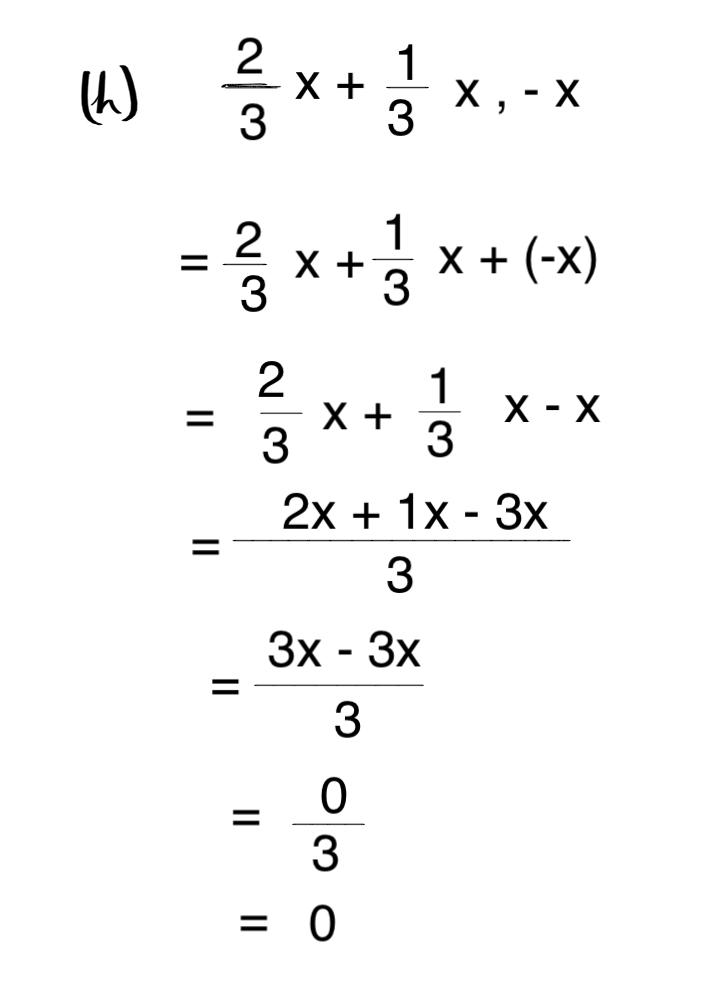
Class 8 Bihar Board Math Solution प्रश्न 2.
पहले व्यंजक में से दूसरे को घटाइए-

(a) 22x , 10x
(b) 17xy , 19xy
(c) a² + 1 , -2a
(d) 8x , -8x
(e) 7xy , 7xy
(f) 7.3x , 1.3x
(g) -6x + y + 4z – 8 , -2y + x – 5z + 8
(h) x/2 − x/4 , x/3

हल:-
(a) 22x , 10x
= 22x – 10x
= 12x
(b) 17xy , 19xy
=17xy – 19xy
= -2xy
(c) a² + 1 , -2a
= a² + 1 – (-2a)
= a² + 2a + 1
(d) 8x , -8x
= 8x – (-8x)
= 8x + 8x
= 16x

(e) 7xy , 7xy
= 7xy – 7xy
= 0
(f) 7.3x , 1.3x
= 7.3x – 1.3x
= 6x
(g) -6x + y + 4z – 8 , -2y + x – 5z + 8
= -6x + y + 4z – 8 – (-2y + x – 5z + 8)
= -6x + y + 4z – 8 + 2y – x + 5z – 8
= -6x – x + y + 2y + 4z + 5z – 8 – 8
= -7x + 3y + 9z – 16

Bihar Board 8th Class Math Solution प्रश्न 3.
सरल कीजिए –
(a) 2x – 3y – 7x + 2x – y + 2
(b) 5y³ – 3y² + 2y – 1 + 2y² + 6y – 5
(c) 6a – 3b + c – 6a + 3b + 7c
(d) 8x² + 5xy + 3y² + 3x² + 2xy – 6y²

हल:-
(a) 2x – 3y – 7x + 2x – y + 2
= 2x + 2x – 7x – 3y – y + 2
= 4x – 7x – 4y + 2
= -3x – 4y + 2
(b) 5y³ – 3y² + 2y – 1 + 2y² + 6y – 5
= 5y³ – 3y² + 2y² + 2y + 6y – 1   – 5
= 5y³ – y² + 8y – 6

(c) 6a – 3b + c – 6a + 3b + 7c
= 6a – 6a – 3b + 3b + c + 7c
= 8c
(d) 8x² + 5xy + 3y² + 3x² + 2xy – 6y²
= 8x² + 3x² + 5xy + 2xy + 3y²  – 6y²
= 11x² + 7xy – 3y²
= 11x² – 3y² + 7xy

Bihar Board Class 8 Math Solution प्रश्न 4.
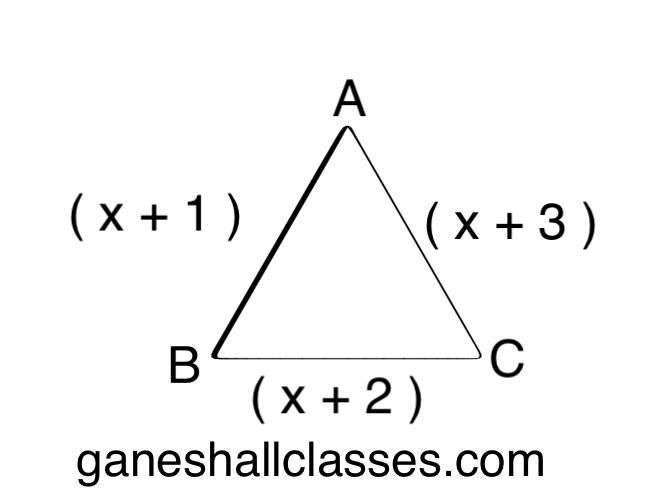
यदि किसी त्रिभुज की भुजाएँ x + 1, x + 2 एवं x + 3 हैं तो इसकी परिमिति क्या होगी?

हल:-
त्रिभुज की भुजाए = (x + 1), (x + 2), (x+3)
त्रिभुज की परिमाप = (x + 1) + (x + 2) + (x+3)
= x + 1 + x + 2 + x+3
= 3x + 6
= 3 ( x + 2 )

Class 8 Maths Bihar Board प्रश्न 5.
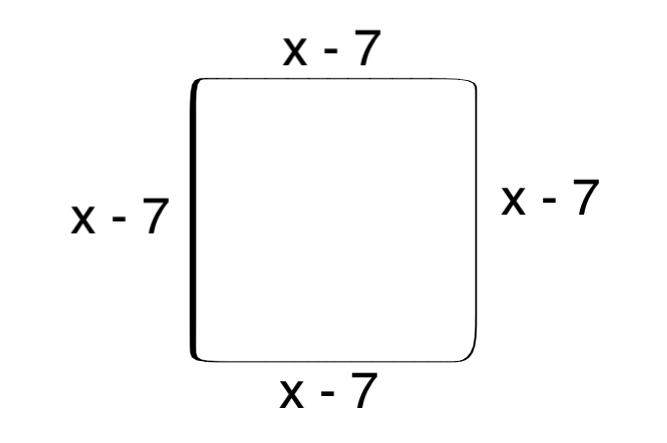
यदि किसी वर्ग की एक भुजा x – 7 है तो उसकी परिमिति ज्ञात कीजिए।

हल:-
वर्ग की भुजा = x-7
वर्ग की परिमाप = 4 x भुजा
= 4 x x-7
= 4x – 28

बीजीय व्यंजक कक्षा 8 गणित Bihar Board प्रश्न 6.
रहीम की उम्र x + 6 वर्ष और महेश की उम्र y वर्ष है, दोनों की उम्र का योग और अंतर क्या होगा?

हल:-
रहीम की उम्र = x – 7
रमेश की उम्र = y
दोनों का योग = x – 6 + y
= x + y – 6
दोनों का अंतर = x – 6 – y
= x – y – 6

Bihar Board Math Solution Class 8 प्रश्न 7.
किसी आयत की दो आसन्न भुजाएँ क्रमशः x² + 2x + 1 एवं x² – 2x + 1 हैं तो आयत की परिमिति क्या होगी?

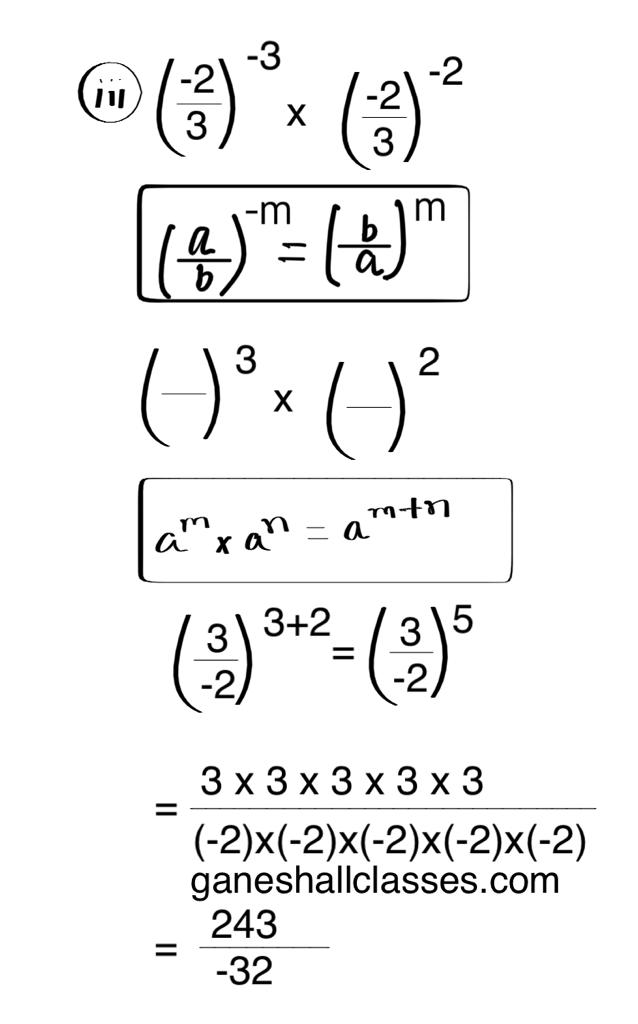
हल:-
आयत की लम्बाई = x² + 2x + 1
आयत की चौड़ाई = x² – 2x + 1
आयत की परिमिति = 2 ( लम्बाई + चौड़ाई )
= 2 ( x² + 2x + 1 + x² – 2x + 1 )
= 2 ( x² + 2 )
= 4x² + 4
= 4 ( x² + 1 )

Bihar Board Class 8 Math Solution In Hindi प्रश्न 8.
किसी त्रिभुज की दो भुजाएँ क्रमश: x², y² हैं। यदि परिमिति x² + y² + z² हो तो त्रिभुज की तीसरी भुजा ज्ञात कीजिए।

हल:-
त्रिभुज की पहली भुजाए = x²
त्रिभुज की दूसरी भुजाए = y²
त्रिभुज की परिमिति = x² + y² + z²
त्रिभुज की तीसरी भुजाए = x² + y² + z² – ( x² + y² )
= x² + y² + z² – x² – y²
= z²

Bihar Board Class 8 Maths Solutions Chapter 9 बीजीय व्यंजक

Bihar Board Class 8 Math Solution बीजीय व्यंजक Ex 9.2

Bihar Board Class 8 Math प्रश्न 1.
गुणनफल ज्ञात कीजिए

(a) 8x × (-2)
(b) -3x × -3x²y
(c) 6mn × 7np
(d) 4p³ × 3p³
(e) x²y × xyz
(f) 2.5x × 4x
(g) 2.5x × 2.5y
(h) 1/2x × 1/2y
(i) 1/2xy × 2xy
(j) 2x × 2x² × 2x³
(k) -3x²y × (-6) × 7xy

हल:-
(a) 8x × (-2)
= 8 × x (-2)
= 8 × (-2) × x
= -16x
(b) -3x × -3x²y
= (-3) × x × (-3) × x × x × y
= (-3) × (-3) × x × x × y
= 9x³y
(c) 6mn × 7np
= 6 x m x n x 7 x n x p
= (6×7) x m x n x n x p
= 42mn²p
(d) 4p³ × 3p³
= 4 x p x p x p x 3 x p x p x p
= (4×3) x p x p x p x p x p x p
= 12p⁶

(e) x²y × xyz
= x × x × y × x × y × z
= x³y²z
(f) 2.5x × 4x
= 2.5 × x × 4 × x
= 2.5 × 4 × x × x
= 10x²
(g) 2.5x × 2.5y
= 2.5× x × 2.5× y
= 2.5× 2.5 × x × y
= 6.25xy

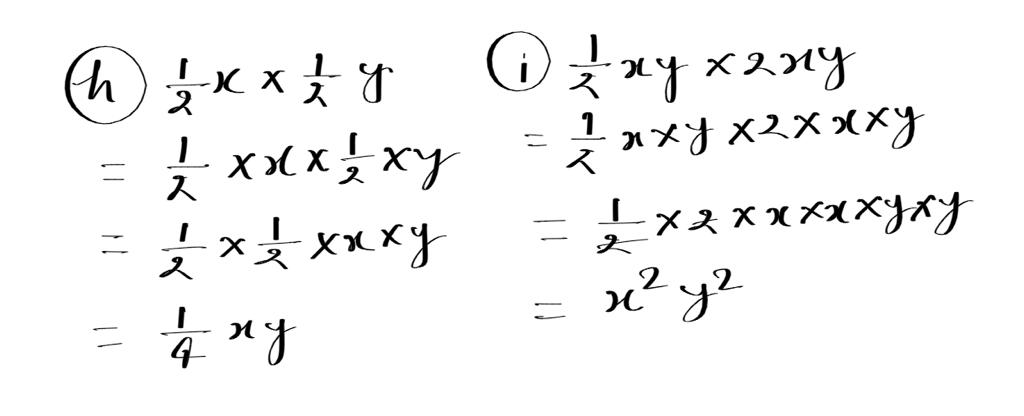
(j) 2x × 2x² × 2x³
= 2 × x × 2 × x × x × 2 × x × x × x
= 2 × 2 × 2 × x × x × x × x × x × x
= 8x⁶
(k) -3x²y × (-6) × 7xy
= -3 × x × x × y × (-6) × 7 × x × y
= -3 × (-6) × 7 × x × x × x × y × y
= 126x³y²

Class 8 Math Solution Bihar Board प्रश्न 2.
किसी आयत की आसन्न भुजाएँ क्रमश: 6p²q² एवं 2pq हैं तो आयत का क्षेत्रफल क्या होगा?

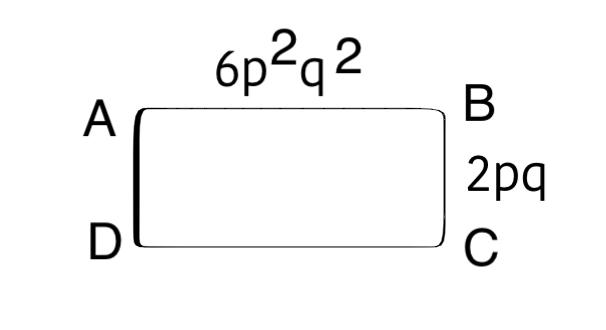
हल:-
आयत का लम्बाई = 6p²q²
आयत का चौड़ाई = 2pq
आयत का क्षेत्रफल = लम्बाई x चौड़ाई
= 6p²q² x 2pq
= 6 × p × p × q × q × 2 × p × q
= 12p³q³

Bihar Board 8 Class Math Solution प्रश्न 3.
यदि किसी वर्ग की भुजा √2 x²y² है तो वर्ग का क्षेत्रफल क्या होगा?

हल:-
वर्ग की भुजा = √2 x²y²
वर्ग का क्षे० = ( भुजा )²
= (√2 x²y²)²
= √2 × √2 × x² × x² × y² × y²
= 2x⁴y⁴

Bihar Board Class 8 Math Solution In Hindi Pdf Download प्रश्न 4.
किसी त्रिभुज का आधार 7xyz एवं संगत शीर्षलंब 2x है तो त्रिभुज का क्षेत्रफल क्या होगा?

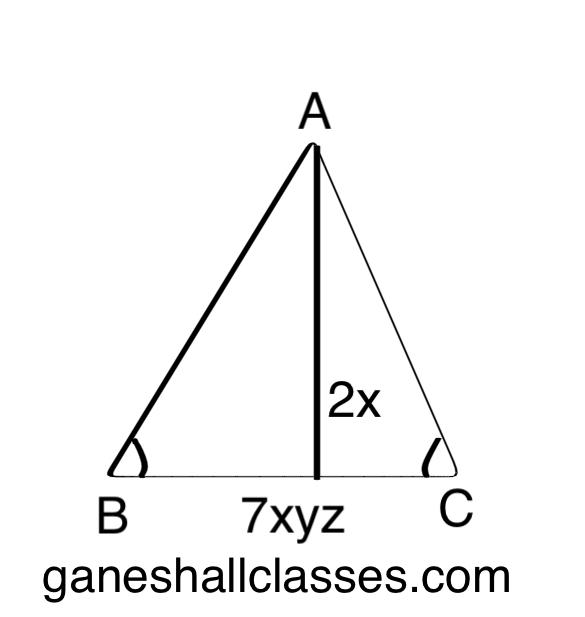
हल:-
त्रिभुज का आधार = 7xyz
त्रिभुज का शीर्षलंब = 2x
त्रिभुज का क्षेत्रफल = 1/2 × आधार × शीर्षलांब
= 1/2 × 7xyz × 2x
= 1/2 × 7 × x × y × z × 2 × x
= 7x²yz

Bihar Board Solution Class 8 Math प्रश्न 5.
समबाहु त्रिभुज का क्षेत्रफल ज्ञात कीजिए यदि उसकी भुजा 3x है।

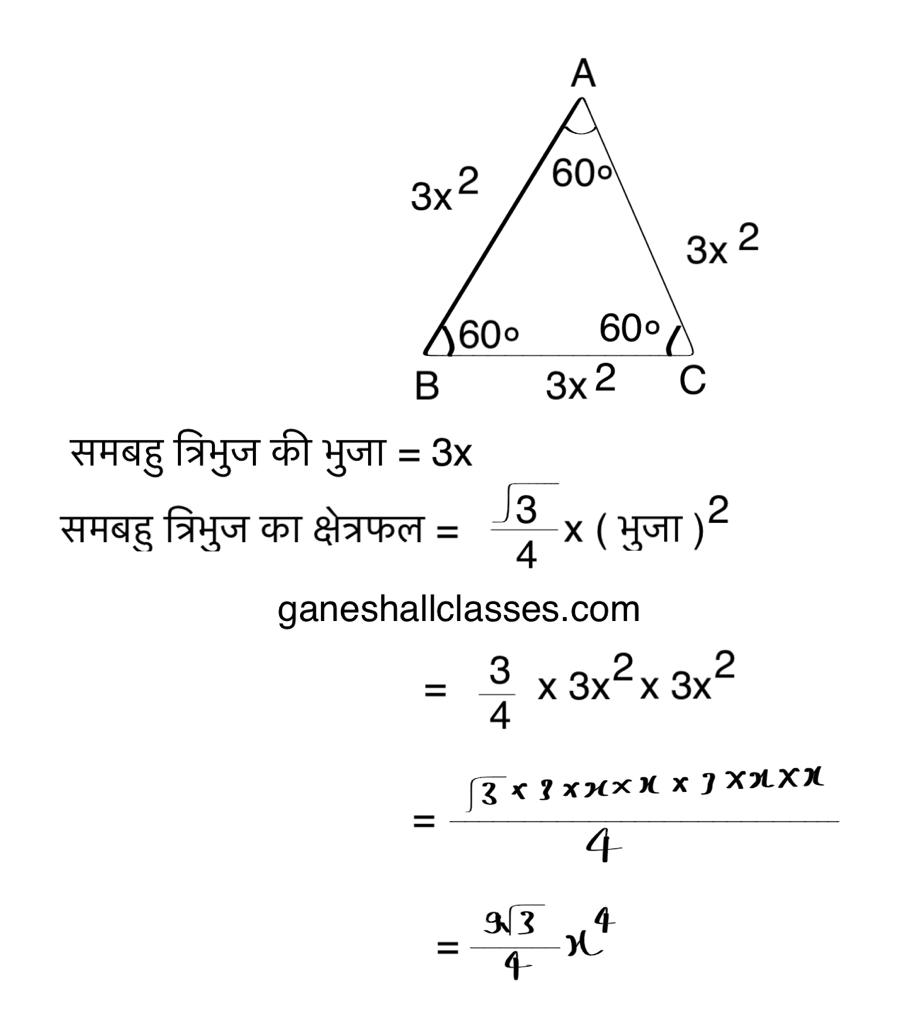
ihar Board Class 8 Maths Solutions प्रश्न 6.
उस घन का आयतन क्या होगा जिसकी कोर 6a हो?

हल:-
घन का कोर(भुजा) = 6a
घन का आयतन = (भुजा)³
= (6a)³
= 6a x 6a x 6a
= 216a³

Bihar Board Solution.Com Class 8 प्रश्न 7.
यदि एक कलम का मूल्य x²y हो तो y²x कलम का मूल्य क्या होगा?

1 कलम का मूल्य = x²y
y²x कलम का मूल्य = x²y × y²x
= x × x × y × y × y × x
= x³y³

Bihar Board Class 8th Math Solution प्रश्न 8.
यदि कोई व्यक्ति x²/2 km/h की चाल से चल रहा हो तो 2 घंटे में वह कितनी दूरी तय कर लेगा?

हल:-
1 घंटे में तय की गई दूरी = x²/2 km
2 घंटे में तय की गई दूरी = x²/2 × 2 km
= x²

Bihar Board Class 8 Math Solution In Hindi बीजीय व्यंजक Ex 9.3

Class 8 Maths Bihar Board Solution प्रश्न 1.
दिए गए बीजीय व्यंजकों का गुणा कीजिए-
(a) (4a – 5b) × (2a – 6b)
(b) (1.5x – 0.5y) × (1.5x + 0.5y)
(c) (1/2pq – 3/2q) × (pq – q)
(d) (a + b) × (3x – y)
(e) (a²b² – c²d²) × (a²b² + c²d²)
(f) (2a + 2b + c) (a + b – c²)

हल:-
(a) (4a – 5b) × (2a – 6b)
= 4a (2a-6b) -5b (2a-6b)
= 4a × 2a + 4a × -6b – 5b × 2a – 5b × -6b
= 8a² – 24ab – 10ab + 30b²
= 8a² + 30b² – 34ab
(b) (1.5x – 0.5y) × (1.5x + 0.5y)
= 1.5x × 1.5x + 1.5x × 0.5y – 0.5y × 1.5x – 0.5y × 0.5y
= 2.25x² + 0.75xy – 0.75xy – 0.25y²
= 2.25x² – 0.25y²

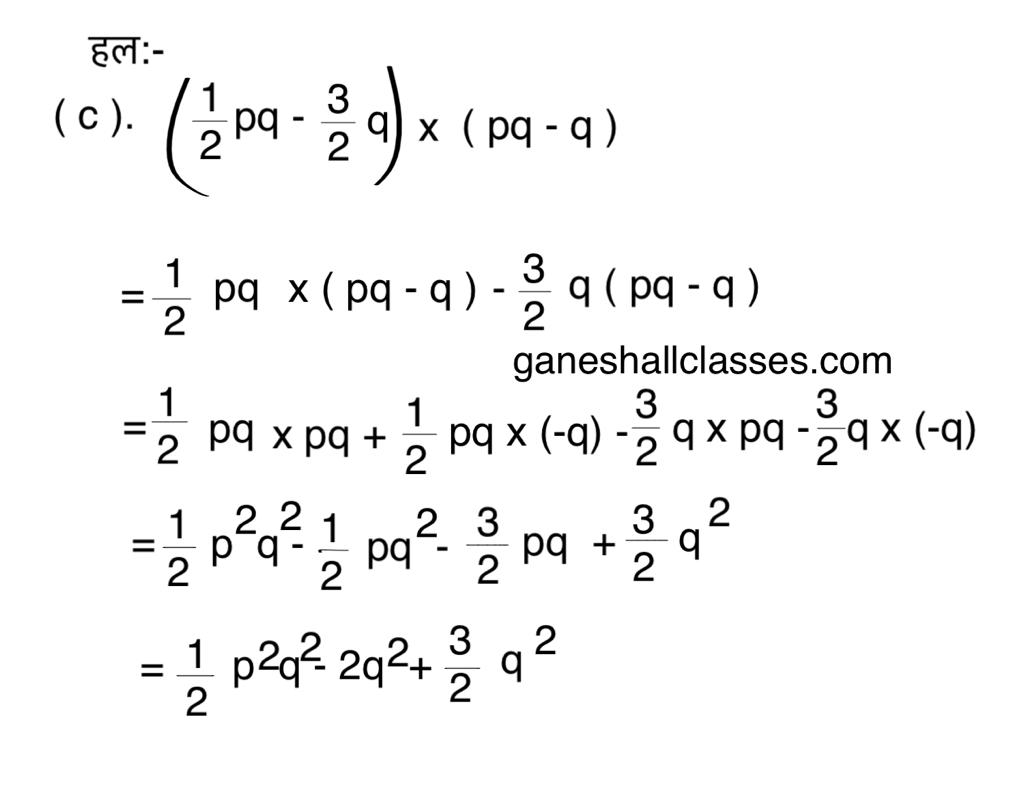
(d) (a + b) × (3x – y)
= a × (3x – y) + b × (3x – y)
= a × 3x – a × y + b × 3x – b × y
= 3ax – ay + 3bx – by
= 3ax – ay + 3bx – by
(e) (a²b² – c²d²) × (a²b² + c²d²)
= a²b² × (a²b² + c²d²) – c²d² × (a²b² + c²d²)
= a²b² × a²b² + a²b² × c²d² – c²d² × a²b² – c²d² × c²d²
= a⁴b⁴ + a²b²c²d² – c²d²a²b² – c⁴d⁴
= a⁴b⁴ – c⁴d⁴
(f) (2a + 2b + c) (a + b – c²)
= 2a × (a + b – c²) 2b × (a + b – c²) c × (a + b – c²)
= 2a × a + 2a × b – 2a × c² + 2b × a + 2b × b – 2b × c² + c × a + c × b – c × c²
= 2a² + 2ab – 2ac² + 2ab + 2b² – 2bc² + ac + bc – c³
= 2a² + 4ab – 2ac² + 2b² – 2bc² + ac + bc – c³

प्रश्न 2.
सरल कीजिए-
(a) (a – b)(a + b) – (a + b)(a + b)
(b) (a² – b) (a – b²) + (a – b)²
(c) (2.3x – 1.7y) (2.3x + 1.7y + 5) – 5.29x² + 2.89y²
(d) (a + b)² – (a – b)²
(e) (x + y + z) × (x + y + z)
(f) (a – b) (b – c) + (b – c) (c – a) + (c – a) (a – b)

हल:-
(a) (a – b)(a + b) – (a + b)(a + b)
= a² – b² – {( a + b )²}
= a² – b² – ( a² + 2ab + b² )
= a² – b² – a² – 2ab – b²
= – b⁴ – 2ab
(b) (a² – b) (a – b²) + (a – b)²
= a²  (a – b²) – b (a – b²) + a² + b² – 2ab
= a³ + a²b² – 3ab + b² + b³
(c) (2.3x – 1.7y) (2.3x + 1.7y + 5) – 5.29x² + 2.89y²
= 2.3x (2.3x + 1.7y + 5) – 1.7y (2.3x + 1.7y + 5) – 5.29x² + 2.89y²
= 5.29x² + 3.9xy + 11.5x – 3.91xy – 2.89y² – 8.5y – 5.29x² + 2.8y²
= 11.5x – 8.5y

(d) (a + b)² – (a – b)²
= a² + b² + 2ab – ( a² + b² – 2ab )
= a² + b² + 2ab – a² – b² + 2ab
= 4ab
(e) (x + y + z) × (x + y + z)
= x (x + y + z) y (x + y + z) z (x + y + z)
= x² + xy +xz + xy + y² + yz + xz + yz + z²
= x² + 2xy + 2xz + y² + 2yz + z²
= x² + y² + z² +2xy + 2yz + 2xz
(f) (a – b) (b – c) + (b – c) (c – a) + (c – a) (a – b)
= a (b – c) -b (b – c) +b (c – a) -c (c – a) +c (a – b) -a (a – b)
= ab – ac – b² + bc + bc – ab – c² + ac + ac – bc – a² + ab
= -b² + bc – c² + ac – a² + ab
= bc + ac + ab – a² – b² – c²

प्रश्न 3.
किसी त्रिभुज का आधार एवं संगत शीर्षलम्ब क्रमशः (x + y)² एवं (x + y)² हैं तो उसका क्षेत्रफल क्या होगा?

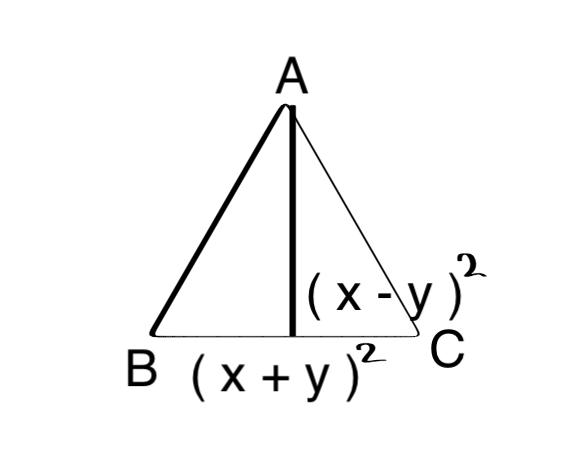
हल:-
त्रिभुज आधार = (x+y)²
त्रिभुज का शीर्षलम्ब = (x-y)²
त्रिभुज का क्षेत्रफल = 1/2 × आधार × शीर्षलम्ब
= 1/2 × (x+y)² × (x-y)²
= 1/2 × ( x² + y² + 2xy ) ( x² + y² – 2xy )
= x² ( x² + y² – 2xy ) + y² ( x² + y² – 2xy ) + 2xy ( x² + y² – 2xy )
= 1/2x⁴ + x²y² – 2x³y + x²y² + y⁴ – 2xy³ + 2x³y + 2xy³ – 4x²y²
= 1/2 × (x⁴ – 2x³y + x²y² + 2x³y – 4x²y² + 2xy³ + x²y² – 2xy³ + y⁴)
= 1/2 × (x⁴ – 2x²y² + y⁴)

प्रश्न 4.
आयत की लम्बाई उसकी चौड़ाई से (x + y) इकाई अधिक है। यदि चौड़ाई z इकाई हो तो आयत की लम्बाई व क्षेत्रफल के लिए व्यंजक लिखिए।

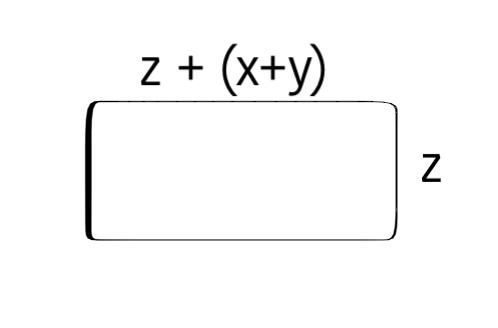
हल:-
आयत की चौड़ाई = z
आयत की लम्बाई = z + (x+y)
= ( x + y + z )
आयत की क्षेत्रफल = लम्बाई x चौड़ाई
= ( x + y + z ) × z
= xz + yz + z²

प्रश्न 5.
यदि किसी लड़की ने (x + y) रु. प्रति किलो की दर से (m + n) किलोग्राम आलू एवं y रुपये प्रति किलोग्राम की दर से (m – n) किलो टमाटर खरीदे तो उसके कुल कितनी राशि देनी होगी?

हल:-
1 किलोग्राम आलू का मूल्य = (x+y)
(m+n) किलोग्राम आलू का मूल्य = (x+y) (m+n)
= x (m+n) +y (m+n)
= mx + nx + my + ny
अब ,
1 किलोग्राम टमाटर का मूल्य = y रु
(m-n) किलोग्राम टमाटर का मूल्य = y x (m-n)
= ym – yn
कुल राशि = mx + nx + my + ny + ym – yn
= mx + nx + 2my

प्रश्न 6.
पिता की उम्र उसके पुत्र की उम्र के (m + n) गुणा है। यदि पुत्र की उम्र (x² – y²) वर्ष हो तो पिता की उम्र के लिए व्यंजक लिखिए।

हल:-
पुत्र का उम्र = (x²-y²)
पिता का उम्र = (x²-y²) + (m+n)
= x² (m+n) -y² (m+n)
= mx² + nx² + my² – ny²

Bihar Board Class 8 Maths Solution बीजीय व्यंजक Ex 9.4

प्रश्न 1.
उचित सर्वसमिकाओं का उपयोग कर दिए गए व्यंजकों का गुणनफल प्राप्त कीजिए-
(a) (5x + 7y)²
(b) (a + a/2)²
(c) (1.5x + 2.5y)²
(d) (x + 1/x)²
(e) (0.4a – 0.5b) (0.4a – 0.5b)
(f) (1/3a+2/3b)(1/3a+2/3b)
(g) (y² – y) (y² – y)
(h) (pqr – 3) (pqr + 3)
(i) (2x + 3) (2x – 5)
(j) (3.5x – y) (3.5x – y)
(k) (x/2−y/2)²
(l) (1/x−1/y)²
(m) (x−1/x)²

हल:-
(a) (5x + 7y)²
सूत्र से ,
(a + b)² = a² + 2ab + b²
a = 5x , b = 7y
(5x + 7y)² = (5x)² + 2 × 5x × 7y + (7y)²
= 25x² + 70xy + 49y²

(c) (1.5x + 2.5y)²
सूत्र से ,
(a + b)² = a² + 2ab + b²
a = 1.5x , b = 2.5y
(1.5x + 2.5y)² = (1.5x)² + 2 × 1.5x × 2.5y + (2.5y)²
= 2.25x² + 7.5xy + 6.25y²

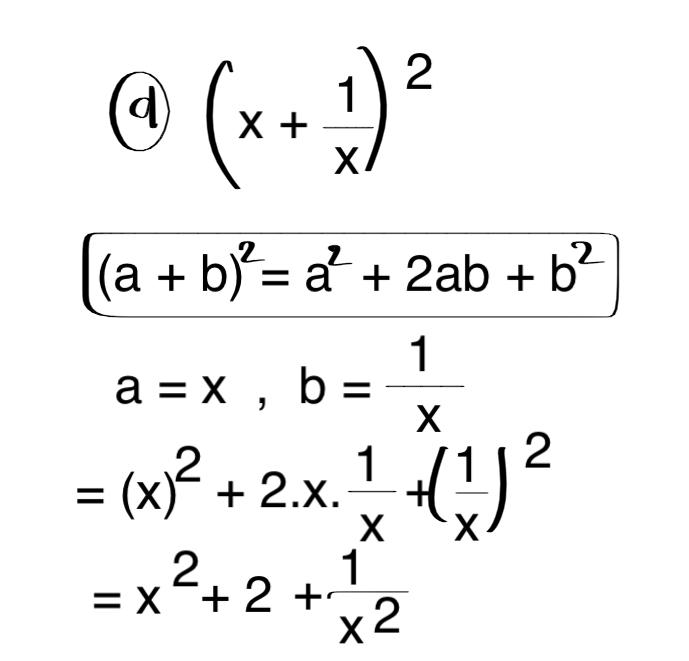
(e) (0.4a – 0.5b) (0.4a – 0.5b)
या (0.4a – 0.5b)²
सूत्र से ,
(a – b)² = a² – 2ab + b²
a = 0.4a , b = 0.5b
(0.4a – 0.5b) = (0.4a)² – 2 × 0.4a × 0.5b (0.5b)²
= 0.16a² – 0.4ab + 0.25b²

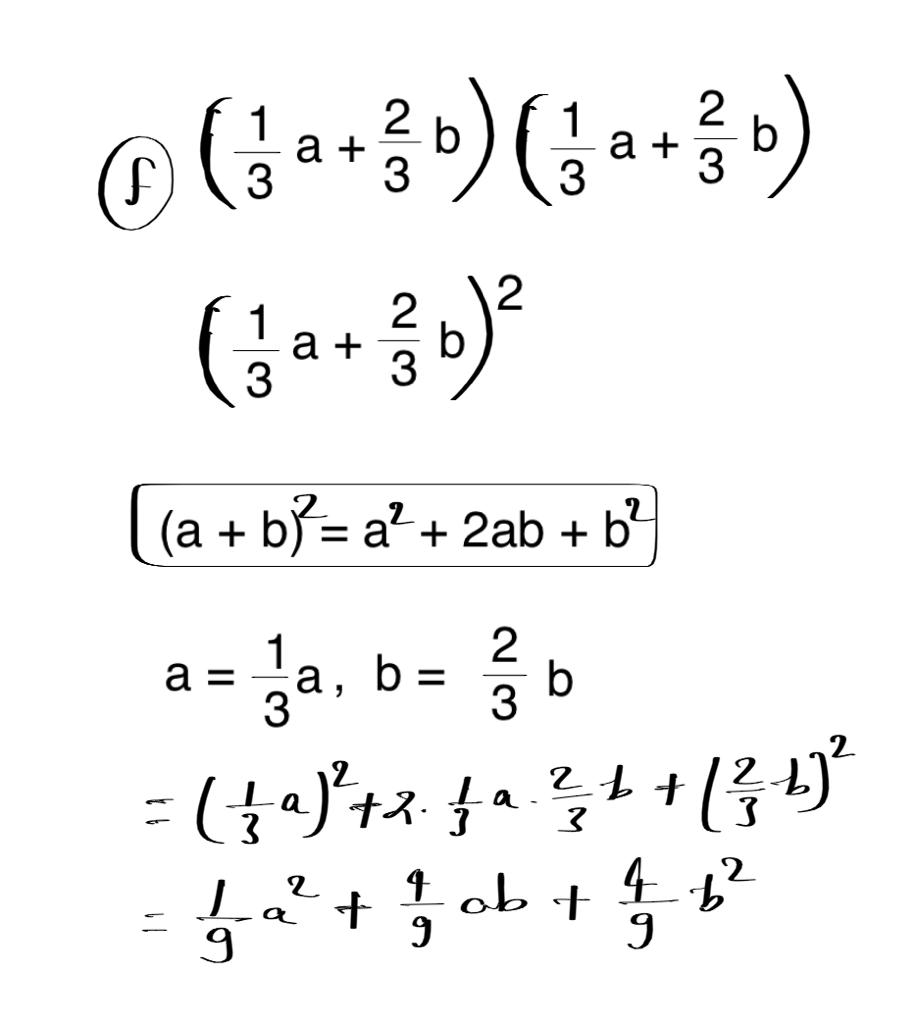
(g) (y² – y) (y² – y)
या (y² – y)²
सूत्र से ,
(a – b)² = a² – 2ab + b²
a = y² , b = y
(y² – y)² = (y²)² – 2 × y² × y + (y)²
= y⁴ – 2y³ + y²
(h) (pqr – 3) (pqr + 3)
सूत्र से ,
(a + b)(a – b) = a² – b²
a² = pqr , b² = 3
(pqr – 3) (pqr + 3) = (pqr)² – 3²
= p²q²r² – 9
(i) (2x + 3) (2x – 5)
सूत्र से ,
(x+a) (x+b) = x² + (a+b)x + ab
x² = 2x , a = 3 , b = (-5)
= (2x)² + ( 3 + (-5) ) 2x + 2 x (-5)
= 4x² + (3-5) 2x – 15
= 4x² – 4x – 15
(j) (3.5x – y) (3.5x – y)
या (3.5x – y)²
सूत्र से
(a – b)² = a² – 2ab + b²
a = 3.5x , b = y
(3.5x – y)² = (3.5x)² – 2 × 3.5x × y + (y)²
= 12.25x² – 7xy + y²

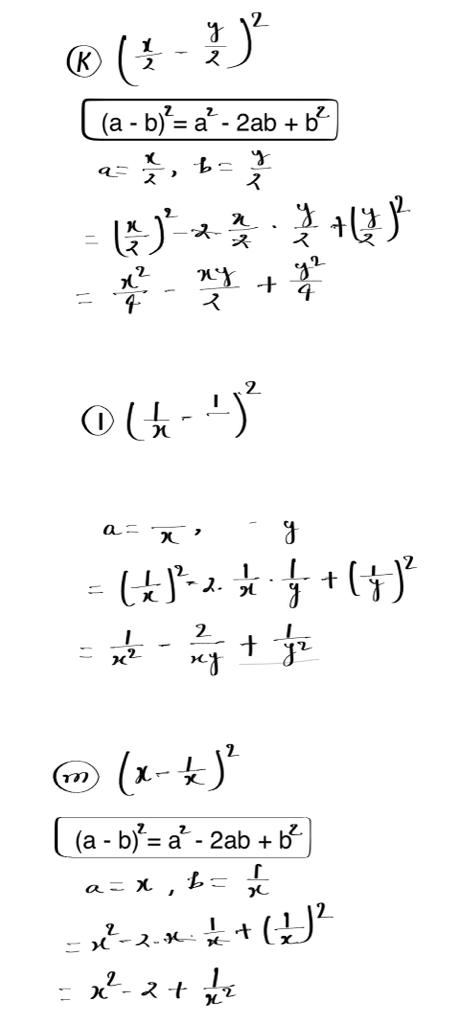
प्रश्न 2.
सरल कीजिए-
(a) (x² + y²)²
(b) (3a – 5b)² – (3a + 5b)²
(c) (xyz + xy)² – 2x²y²z

हल:-
(a) (x² + y²)²
सूत्र से
(a + b)² = a² + 2ab + b²
a = x² , b = y²
(x² + y²)² = (x²)² + 2 × x² × y² (y²)²
= x⁴ + 2.x²y² + y4
(b) (3a – 5b)² – (3a + 5b)²
सूत्र से
(a + b)² = a² + 2ab + b²
या (a – b)² = a² – 2ab + b²
= (3a)² – 2(3a) (5b) + (5b)² – {(3a)² + 2(3a) (5b) +(5b)²}
= 9a² – 30ab + 25b² – {9a² + 30ab + 25b²}
= 9a² – 30ab + 25b² – 9a² – 30ab – 25b²
= -60ab
(c) (xyz + xy)² – 2x²y²z
सूत्र से
(a + b)² = a² + 2ab + b²
a = xyz , b = xy
= ( xyz)² + 2हल:-
(a) (x² + y²)²
सूत्र से
(a + b)² = a² + 2ab + b²
a = x² , b = y²
(x² + y²)² = (x²)² + 2 × x² × y² (y²)²
= x⁴ + 2.x²y² + y4
(b) (3a – 5b)² – (3a + 5b)²
सूत्र से
(a + b)² = a² + 2ab + b²
या (a – b)² = a² – 2ab + b²
= (3a)² – 2(3a) (5b) + (5b)² – {(3a)² + 2(3a) (5b) +(5b)²}
= 9a² – 30ab + 25b² – {9a² + 30ab + 25b²}
= 9a² – 30ab + 25b² – 9a² – 30ab – 25b²
= -60ab
(c) (xyz + xy)² – 2x²y²z
सूत्र से
(a + b)² = a² + 2ab + b²
a = xyz , b = xy
= ( xyz)² + 2 × xyz × xy + (xy)² – 2x²y²z
= x²y²z² + 2x²y²z + x²y² – 2x²y²z
= x²y²z² + x²y²

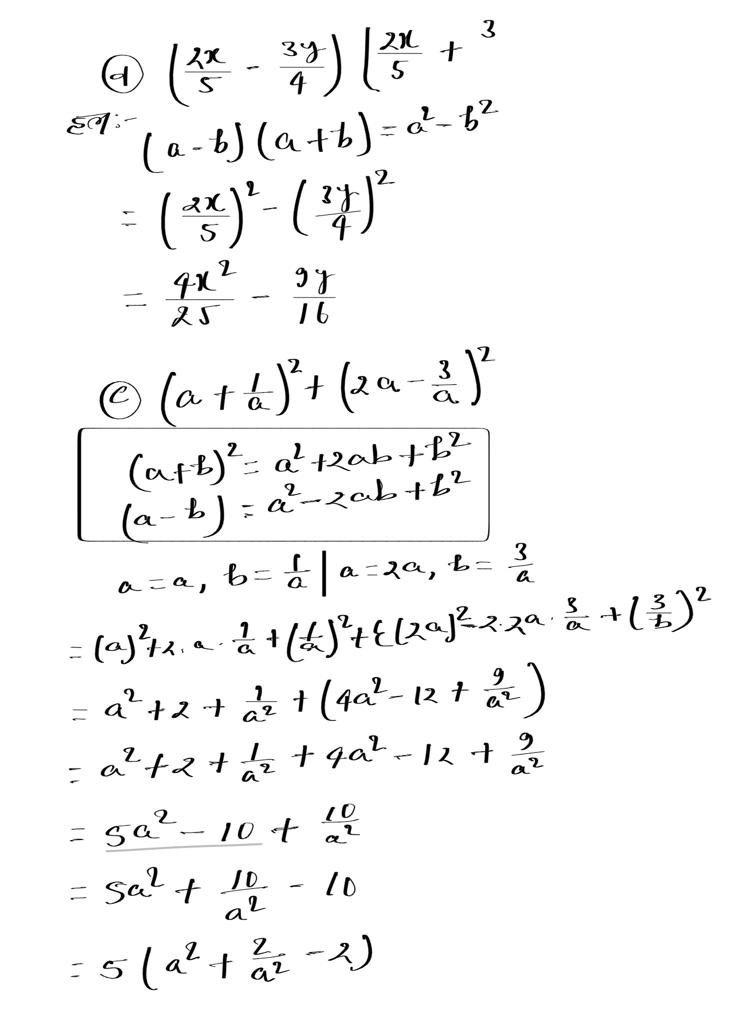
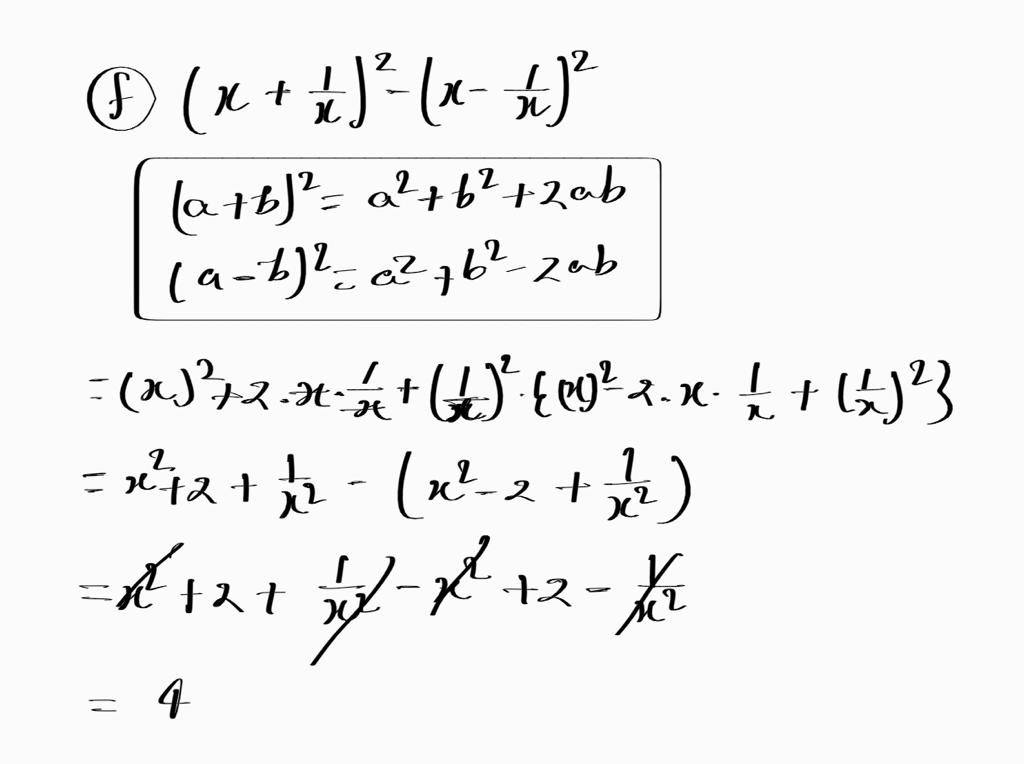
प्रश्न 3.
सर्वसमिकाओं के उपयोग से निम्नलिखित मान ज्ञात कीजिए
(a) 812
(b) (999)
(c) (52)
(d) (498)
(e) (5.5)²
(f) 191 × 209
(g) 10.5 × 9.5
(h) (101)² – (99)²
(i) (1.5)² – (0.5)²

हल:-
(a) 81²
= (80 + 1)²
सूत्र से ,
(a + b)² = a² + 2ab + b²
= (80)² + 2 × 80 × 1 + 1²
= 6400 + 160 + 1
= 6561
(b) (999)²
 = (1000 – 1)²
सूत्र से ,
(a – b)² = a² – 2ab + b²
= (1000)² – 2 × 1000 × 1 + 1²
= 1000000 – 2000 + 1
= 998001
(c) (52)²
= (50 + 2)²
सूत्र से ,
(a + b)² = a² + 2ab + b²
= (50)² + 2 × 50 × 2 + 2²
= 2500 + 200 + 4
= 2704
(d) (498)²
= (500 – 2)²
सूत्र से ,
(a – b)² = a² – 2ab + b²
= (500)² – 2 × 50 × 2 + 2²
= 250000 – 2000 + 4
= 250004 – 2000
= 248004
(e) (5.5)² 
= (6 – 0.5)²
सूत्र से ,
(a – b)² = a² – 2ab + b²
= 6² – 2 × 6 × 0.5 + (0.5)²
=36 – 6 + 0.25
= 36.25 – 6
= 30.25

(f) 191 × 209
= (200 – 9) × (200 + 9)
सूत्र से ,
(a-b) (a+b) = a² – b²
= (200)² – 9²
= 40000 – 81
= 39919
(g) 10.5 × 9.5
= (10 + 0.5) × (10 – 0.5)
सूत्र से ,
(a+b) (a-b) = a² – b²
= (10)² – (0.5)²
= 100 – 0.25
= 99.75
(h) (101)² – (99)²
सूत्र से ,
(a-b) (a+b) = a² – b²
= (101 + 99) (101 – 99)
= (200) (2)
= 400
(i) (1.5)² – (0.5)²
सूत्र से ,
(a-b) (a+b) = a² – b²
= (1.5 + 0.5) (1.5 – 0.5)
= 2 × 1
= 2

प्रश्न 4.
सर्वसमिका (x + a) (x + b) = x² + (a + b)x + ab का उपयोग कर निम्नलिखित का गुणनफल एवं मान ज्ञात कीजिए-
(a) (x + 3y) (x + 5y)
(b) (3x + 7) (3x + 5)
(c) (x – 5)(x + 4)
(d) (2x – 7) (2x – 9)
(e) 52 × 53
(f) 3.1 × 3.2

(a) (x + 3y) (x + 5y)
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= x² + (3y + 5y)x + 3y × 5y
= x² + (8y)x + 15y²
= x² + 8xy + 15y²
(b) (3x + 7) (3x + 5)
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= (3x)² + (7 + 5)3x + 7 × 5
= 9x² + 36x + 35
(c) (x – 5) (x + 4)
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= x² + (-5 + 4)x + (-5) (4)
= x² – x – 20

(d) (2x – 7) (3x – 9)
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= (2x)² + (-7 – 9) 2x + (-7) (-9)
= 4x² – 32x – 63
(e) 52 × 53
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= (50 + 2) (50 + 3)
= (50)² + (2 + 3) 50 + 2 × 3
= 2500 + 250 + 6= 2756
(f) 3.1 × 3.2
सर्वसमिकाए : (x+a)(x+b) = x² + (a+b)x +ab
= (3 + 0.1) (3 + 0.2)
= 3² + (0.1 + 0.2)3 +0.1 × 0.2
= 9 + (0.3)3 + 0.02
= 9 + 0.9 + 0.02
= 9.92