Bihar Board Class 8 Math Solution Chapter 14 गुणनखंड(factor)

Bihar Board Class 8 Maths Solutions Chapter 14 गुणनखंड (factor)Text Book Questions and Answers.

Bihar Board Class 8 Math Solution Chapter 14 गुणनखंड (factor)

bseb class 8 math solution

Bihar Board Class 8 Math Solution गुणनखंड Ex 14.1

गुणनखंड ज्ञात कीजिए Class 8 Bihar Board प्रश्न 1.
दिए गए पदों में सार्व (उभयनिष्ठ) गुणनखंड ज्ञात कीजिए-

(a) 9y, 27
(b) 5x, 25x
(c) 7ab, -14ab
(d) -16x²y², -x²y²z²
(e) 17x, 102y
(f) 11xyz, 100z
(g) a²bc, ab²c, abc²
(h) 2x, 3y, 5z
(i) 20x²y², 30y²z², 40z²x²
(j) 2x (a + b)(b + c), x (a + b)

हल :-
(a) 9y, 27
9y = 3 × 3 × y
27 = 3 × 3 × 3
सार्व (उभयनिष्ठ) गुणनखण्ड 
 3 × 3 = 9

(b) 5x, 25x
5x = 5 × x
25x = 5 × 5 × x
सार्व गुणनखण्ड 
= 5x

(c) 7ab, -14ab
7ab = 7 × a × b
-14ab = -2 × 7 × a × b
सार्व गुणनखण्ड
= 7ab

(d) -16x²y², -x²y²
-16x²y² = -(2 × 2 × 2 × 2 × x × x × y × y)
-x²y²z² = -(x × x × y × y × z × z)
सार्व गुणनखण्ड 
-( x × x × y × y) = x²y²

(e) 17x, 102y
17x = 17 × x
102y = 6 × 17 × y
सार्व गुणनखण्ड 
= 17

(f) 11xyz, 100z
11xyz = 11 × x × y × z
100z = 2 × 2 × 5 × 5 × z
सार्व गुणनखण्ड
= z

(g) a²bc, ab²c, abc²
a²bc = a × a × b × c
ab²c = a × b × b × c
abc² = a × b × c × c
सार्व गुणनखंड 
 a × b × c = abc

(h) 2x, 3y, 5z
2x = 2 × x × 1
3y = 3 × y × 1
5z = 5 × z × 1
सार्व गुणनखंड
= 1

(i) 20x²y², 30y²z², 40z²x²
20x²y² = 2 × 2 × 5 × x × x × y × y
30y²z² = 2 × 3 × 5 × y × y × z × z
40z²x² = 2 × 2 × 2 × 5 × z × z × x × x
सार्व गुणनखण्ड
2 × 5 = 10

(j) 2x (a + b)(b + c), x (a + b)
 2x (a + b) (b + c) = 2 × x × (a + b) × (b + c)
x (a + b) = x × (a + b)
सार्व गुणनखण्ड
= x(a + b)

क्र. सं	पद	अलग किया गया गुणनखंड	शेष गुणनखंड
i.	12x2y	3x	4xy
ii.	15ab	-3	……….
iii.	-20xy	-2xy	……….
iv.	40x2y2	…………..	-20
v.	-27abc	…………..	-3ab

क्र. सं	पद	अलग किया गया गुणनखंड	शेष गुणनखंड
i.	12x2y	3x	4xy
ii.	15ab	-3	-5ab
iii.	-20xy	-2xy	10
iv.	40x2y2	-2x2y2	-20
v.	-27abc	9c

गुणनखंड कक्षा 8 Bihar Board प्रश्न 3.
निम्नलिखित का गुणनखण्ड ज्ञात कीजिए-

(a) 12x² – 15y² – 24x²z²
(b) -6a² + 36a – 24ab
(c) 3a² + ab + 9a + 3b
(d) 6ab – 4b + 6 – 9a
(e) ab² + a²b + ac + bc
(f) a²bc + b²ca + c²ab + a + b + c
(g) a(b – c) + d (c – b)
(h) 3y(y + 3) + 6y(3y + 9)
(i) a³ – 3a² + a – 3
(j) ab² – bc² – ab + c²
(k) xy (a² + b²) + ab (x² + y²)

हल :-
(a) 12x² – 15y² – 24x²z²
= 2 × 2 × 3 × x × x – 3 × 5 × y × y – 2 × 2 × 2 × 3 × x × x × z × z
= 3(4x² – 5y² – 8x²z²)

(b) -6a2 + 36a – 24ab
= -2 × 3 × a × a + 2 × 2 × 3 × 3 × a – 2 × 2 × 2 × 3 × a × b
= -6a (a – 6 + 4b)

(c) 3a² + ab + 9a + 3b
= a (3a + b) + 3(3a + b)
= (3a + b) (a + 3)

(d) 6ab – 4b + 6 – 9a
= 2b (3a – 2) – 3 (3a – 2)
= (3a – 2) (2b – 3)

(e) ab² + a²b + ac + bc
= ab (b + a) + c (b + a)
= (b + a) (ab + c)

(f) a²bc + b²ca + c²ab + a + b + c
= abc (a + b + c) + 1 (a + b + c)
= (a + b + c) (abc + 1)

(g) a(b – c) + d (c – b)
= ab – ac + dc – db
= a(b – c) – d(c – b)
= (a – d) (b – c)

(h) 3y (y + 3) + 6y (3y + 9)
= 3y² + 9y + 18y² + 54y
= 21y² + 63y
= 21y (y + 3)

(i) a³ – 3a² + a – 3
= a²(a – 3) + 1 (a – 3)
= (a – 3) (a² + 1)

(j) ab² – bc² – ab + c²
= b(ab – c²) – 1(ab – c²)
= (ab – c²) (b – 1)

(k) xy(a² + b²) + ab (x² + y²)
= xya² + xyb² + abx² + aby²
= ay(ax + by) + bx(ax + by)
= (ay + bx) (ax + by)

Bihar Board Class 8 Math Solution गुणनखंड Ex 14.2

bseb class 8 math solution

Bihar Board Class 8 Math Solution Chapter 14 गुणनखंड(factor)

Bihar Board Class 8 Math Solution प्रश्न 1.
निम्नलिखित व्यंजकों का गुणनखंड ज्ञात कीजिए-

(a) 1 + 2x + x²
(b) a²b² – 6abc + 9c²
(c) 1 – (a – b)²
(d) 16 (a – b)² – 9 (a + b)
(e) (x + y)² – 10 (x + y) + 25
(f) (a + b)² – 4ab
(g) 4x² – y²+ 4y – 4
(h) 9x² – n²/4
(i) a² + a + 4 + 3a
(j) x² + 6x + 8
(k) y² – 13y + 30
(l) x² + 9x – 22

हल :-
(a) 1 + 2x + x²
सर्वसमिका (सूत्र) का प्रयोग करके,
(a+b)² = a² + 2ab + b²
= (1)² + 2.1.x + (x)²
= (1+x)²
= (1+x) (1+x)

(b) a²b² – 6abc + 9c²
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – 2ab + b² = (a-b)²
= (ab)² – 2.ab.3c + (3c)²
= (ab – 3c)²
= (ab – 3c) (ab – 3c)

(c) 1 – (a – b)²
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – b² = (a+b) (a-b)
= (1)² – (a-b)²
= [ 1 + (a-b) ] [ 1 – (a-b) ]
= ( 1 + a – b ) ( 1 – a + b )

(d) 16 (a – b)² – 9 (a + b)
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – b² = (a+b) (a-b)
= (4)² ( a-b)² – (3)² ( a + b )²
= [{4(a-b)}² – { 3 (a+b)}²]
= ( 4a – 4b )² – ( 3a + 3b )²
a² – b² = (a+b) (a-b)
= (4a-4b + 3a+3b) ( 4a-4b – (3a-3b)
= (7a – b) (a – 7b)

(e) (x + y)² – 10 (x + y) + 25
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – 2ab + b² = (a-b)²
= (x+y)² – 2.(x+y).5 + (5)²
= (x + y – 5)²
= (x + y – 5) (x + y – 5)

(f) (a + b)² – 4ab
सर्वसमिका (सूत्र) का प्रयोग करके,
(a+b)² = a² + 2ab + b²
= a² + 2ab + b² – 4ab
= a² – 2ab + b²
= (a-b)²
= (a-b) (a-b)

(g) 4x² – y²+ 4y – 4
= (4x² – (y² – 4y + 4)
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – 2ab + b² = (a-b)²
= 4x² – { (y)² – 2.y.2 + (2)²}
= (2x)² – (y-2)²
a² – b² = (a+b) (a-b)
= [ (2x + (y-2)] [ (2x – (y-2)]
= (2x + y – 2 ) (2x – y + 2)

(h) 9x² – n²/4

(i) a² + a + 4 + 3a
= a² + 4a +4
सर्वसमिका (सूत्र) का प्रयोग करके,
(a+b)² = a² + 2ab + b²
= a² + 2.a.2 + (2)²
= (a+2)²
= (a+2) (a+2)

(j) x² + 6x + 8
= x² + 4x + 2x + 8
= x (x+4) +2 (x+4)
= (x+4) (x+2)

(k) y² – 13y + 30
= y² – 10y – 3y + 30
= y (y-10) -3 (y-10)
= (y-10) ( y-3)

(l) x² + 9x – 22
= x² + 11x – 2x – 22
= x (x+11) -2 (x + 11)
= (x + 11) (x-2)

Bihar Board 8th Class Math Solution प्रश्न 2.
निम्नलिखित व्यंजकों का गुणनखण्ड कीजिए-

(a) x² – 6x – 135
(b) 8(x + y)³ – 50(x + y)
(c) 4x² + 9y² + 12xy – 1
(d) 75 – x² + 10x
(e) 12a² – 27
(f) ax² – bx² + by² – ay²

हल :-
(a) x² – 6x – 135
= x² – 15x + 9x – 135
= x (x – 15) + 9 (x – 15)
= (x – 15) (x + 9)

(b) 8(x + y)³ – 50(x + y)
= 2 (x+y) [ 4 (x+y)² – 25]
सर्वसमिका (सूत्र) का प्रयोग करके,
a² – b² = (a+b) (a-b)
= 2 (x+y) [{2(x+y)}² – (5)²]
= 2 (x+y) {2 (x+y) – 5)} { 2 ( x+y) + 5)
= 2 (x+y) (2x+2y-5) ( 2x+2y+5)

(c) 4x² + 9y² + 12xy – 1
सर्वसमिका (सूत्र) का प्रयोग करके,
(a+b)² = a² + 2ab + b²
= (2x)² + (3y)² + 2(2x) (3y) – 1
= (2x + 3y)² (1)
a²-b² = (a+b) (a-b)
= (2x + 3y – 1)  (2x + 3y + 1)

(d) 75 – x² + 10x
= -x² + 10x + 75
= -x² – 5x + 15x + 75
= -x (x + 5) 15 (x + 5)
= (x + 5) (15 – x)

(e) 12a² – 27
= 3 (4a² – 9)
= 3 [ (2a)² – (3)² ]
a² – b² = (a+b) (a-b)
= 3 (2a-3) (2a+3)

(f) ax² – bx² + by² – ay²
= ax² – ay² – bx² + by²
= a (x² – y²) -b (x² – y²)
= (x² – y²) (a – b)
= (x-y) (x+y) (a-b)

Bihar Board Class 8 Math Solution Chapter 14 गुणनखंड(factor)

bseb Class 8 Math Solution प्रश्न 3.
निम्नलिखित व्यंजकों का गुणनखंडन कीजिए-

(a) 16x⁴ – 81y⁴
(b) x⁴ – 1
(c) x⁴ – (x – y)⁴
(d) 9x² – 4y² – 3x + 2y
(e) (x + y) + 4 (x + y)² + 4x + 4y

हल :-
(a) 16x⁴ – 81y⁴
a² – b² = (a+b) (a-b)
= (4x²)² – (9y²)²
= (4x² + 9y²) (4x² – 9y²
a² – b² = (a+b) (a-b)
= [(2x)² – (3y)²] (4x² + 9y²)
= (2x + 3y) (2x – 3y) (4x² + 9y²)

(b) x⁴ – 1
a² – b² = (a+b) (a-b)
= (x²)² – (1)²
= (x² + 1) (x² – 1)
= (x² + 1) (x – 1) (x + 1)
= (x – 1) (x + 1) (x² + 1 )

(c) x⁴ – (x – y)⁴
a² – b² = (a+b) (a-b)
= (x²)² – {(x – y)²}²
= [x² – (x – y)²] [x² + (x-y)²]
a² – b² = (a+b) (a-b)
= (x -(x-y) (x+x-y) [x² + (x-y)²]
= (x-x+y) (x+x-y) [x² + x² + y² – 2.x.y]
= y(2x-y) (2x²+y²-2xy)
(d) 9x² – 4y² – 3x + 2y
a² – b²= (a+b) (a-b)
= (3x)² – (2y)² – 3x + 2y
= (3x – 2y) (3x + 2y) – (3x – 2y)
= (3x – 2y) (3x+2y-1)
(e) (x + y) + 4 (x + y)² + 4x + 4y
= (x+y)³ + 4 (x + y)² + (x + y)
= (x +y) [(x + y)² + 2.(x + y) 2 + (2)²]
= (x + y) (x + y + z) (x + y + z)

Bihar Board Class 8 Math Solution गुणनखंड Ex 14.3

bseb class 8 math solution

Bihar Board Class 8 Math Solution Chapter 14 गुणनखंड(factor)

Class 8 Math Bihar Board प्रश्न 1.
निम्नलिखित का भाग कीजिए-

(a) -2x²yz का 4xyz से
(b) −1/2 xy का x/2 से
(c) (3x²)⁵ का (9x²)³ से
(d) (7x⁵)² × (3y⁵)⁵ का 27y³ से
(e) 8x⁶y⁶ का -4x⁴y⁶ से

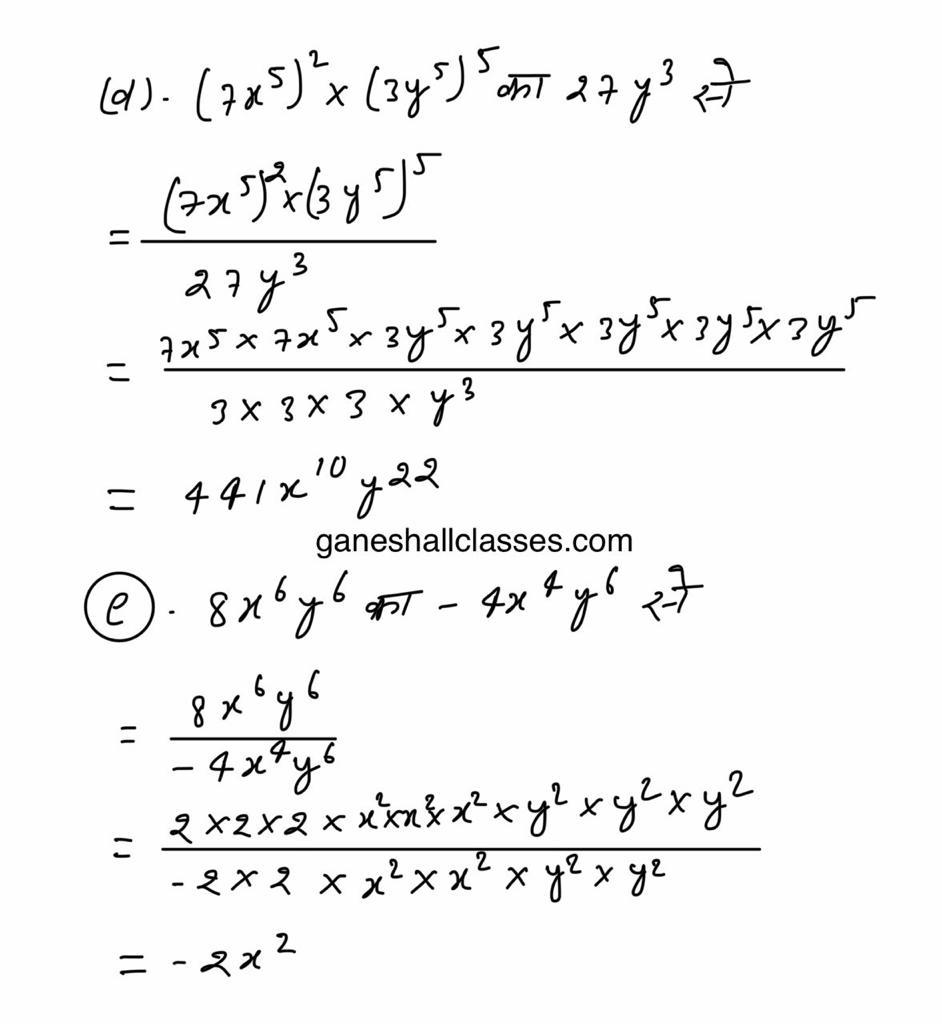
Gunankhand Math Class 8 प्रश्न 2.
दिए गए बहुपद को एकपदी से भाग कीजिए-

(a) (5m³ – 30m²) ÷ 5m
(b) (12x⁴ – 6x²) ÷ (-3x²)
(c) (5x² – 15x) ÷ (x – 3)
(d) (6x⁴ + 9x³ – 12x²) ÷ 3x²

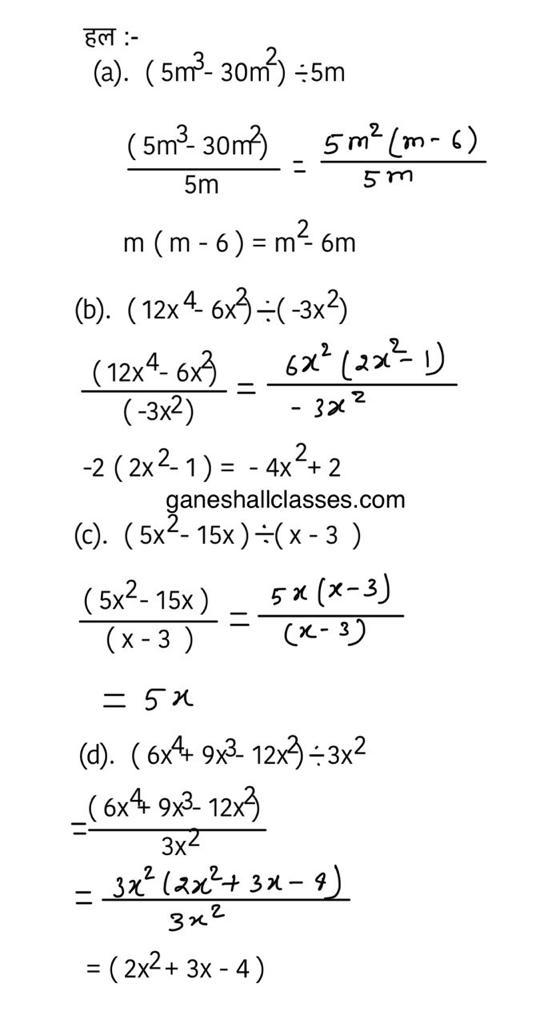
Class 8 Maths Bihar Board प्रश्न 3.
भाग कीजिए-

(a) (a² + 8a + 16) ÷ (a + 4)
(b) {(a + b)² – 4ab} ÷ (a – b)²
(c) (a⁴ – b⁴) ÷ (a² – ab)
(d) (x⁴ – 81) ÷ (x² + 9)
(e) 121x² + 16y² – 88xy ÷( 4y – 11x)
(f) (x² – x – 30) ÷ (x – 6)
(g) {p² – p + 1/4 } ÷ {p – 1/2}
(h) (x² – 5xy + 6y²) ÷ (x – 2y)
(i) (27x³ + 3x² – 2x + 8) ÷ (3x – 2)