Bihar Board Class 8 Maths Solution In Hindi Chapter 2 एक चर वाले रैखिक समीकरण

bihar board class 8 math solution in hindi एक चर वाले रैखिक समीकरण Ex 2.1

Bihar Board Class 8 Math Solution in hindi प्रश्न 1.

निम्नलिखित समीकरणों का हल कीजिए –

1. 3(x – 3) = 15
हल:- पहला विधि ( 1st method )
3(x – 3) = 15
3x – 9 = 15
3x = 15 + 9
3x = 24
x = 24/3
x = 8
दूसरा विधि ( 2nd method )
3(x-3) = 15
3x-9 = 15
3x-9+9 = 15+9
3x/3 = 24/3
x = 8

Bihar Board Class 8 Math Solution Chapter 2 प्रश्न 2.

x/2 – 7 = 15
हल:-
x/2 – 7 = 15
x/2 = 15+7
x/2 = 22
x = 22×2
x = 44

Class 8 Bihar Board Math Solution प्रश्न 3.

−2x/7 + 2 = 8

हल:-
−2x/7 + 2 = 8
-2x/7 = 8-2
या -2x = 6×7
या -2x = 42
या x = 42/2
x = -21

Bihar Board Class 8 Math Solution In Hindi प्रश्न 4.
7 – 3x = 18
हल:-
7 – 3x = 18
7 – 3x = 18
-3x = 18 – 7
-3x = 11
x = −11/3

https://youtube.com/@GaneshAllClassesOfficial?si=h-LjbK_BrTcWHDSW

Bihar Board Math Solution Class 8 प्रश्न 5.

18 = 40 – 3x
हल:-
40-3x = 18
या -3x = 18-40
या -3x = -22
या 3x = 22
x = 22/3

Bihar Board 8th Class Math Solution प्रश्न 6.

25/6 – 9y = 11

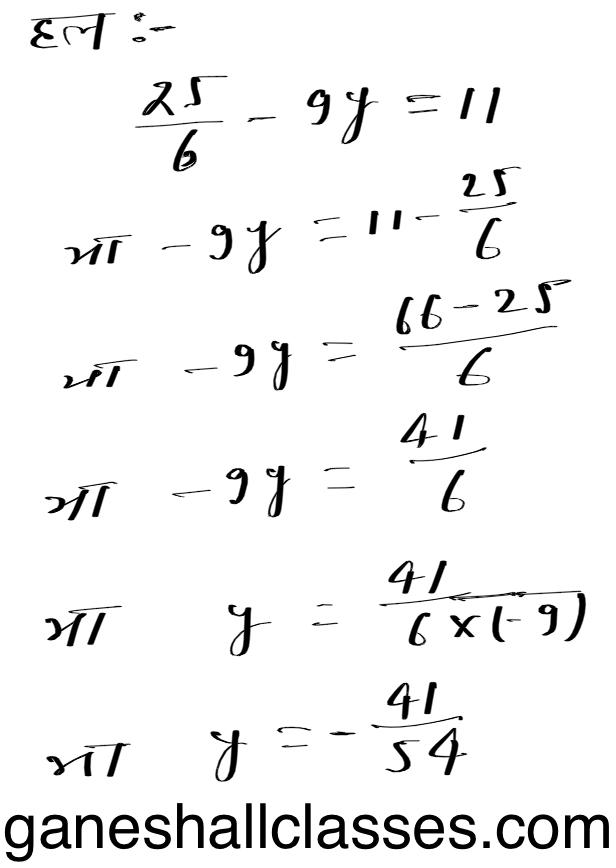
Class 8 Math Solution Bihar Board प्रश्न 7.

2.4 = x/2.5 – 1
हल:-
2.4 = x/2.5 – 1
या x/2.5 -1 = 2.4
या x/2.5 = 2.4 + 1
या x/2.5 = 3.4
या x = 3.4 x 2.5
x = 8.5

Bihar Board Solution Class 8 Math प्रश्न 8.

3x + 10 = 1
हल:-
3x + 10 = 1
या 3x = 1 – 10
या 3x = -9
या x = -9/3
x = -3

Bihar Board Class 8 Math प्रश्न 9.

bihar board class 8 math solution in hindi एक चर वाले रैखिक समीकरण Ex 2.2

Bihar Board Class 8 Math Solution

प्रश्न 1. यदि किसी संख्या आधे में से 1/4 घटाया जाए तो 1/8 प्राप्त होता है । संख्या ज्ञात कीजिए ।

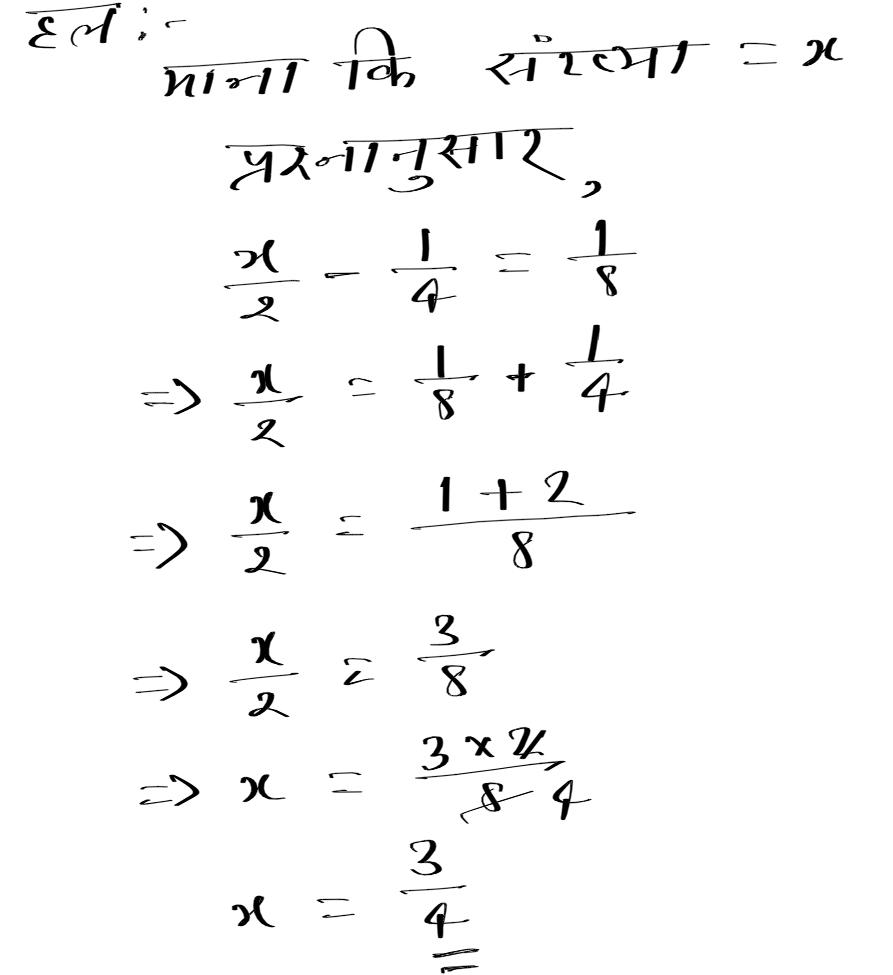
Bihar Board 8 Class Math Solutionप्रश्न 2. यदि किसी आयत की लम्बाई और चौड़ाई का अंतर 5 मी. हो और परिमिति 110 मी. हो तो लम्बाई एवं चौड़ाई ज्ञात करें।
हल:-
माना कि आयत की लम्बाई = x
आयत की चौड़ाई = y
प्रश्नानुसार,आयत की परिमाप = 110 मीटर
सूत्र से,
2( लम्बाई + चौड़ाई ) = 110 मीटर
या 2{ x + (x-2)} = 110 मीटर
या 2( x + x – 2 ) = 110 मीटर
या 2( 2x – 5 ) = 110 मीटर
या 4x – 10 = 110 मीटर
या 4x = 110+10
या 4x = 120
या x = 120/4
x = 30 मीटर
अतः आयत की लम्बाई = 30 मीटर आयत की चौड़ाई = 30 – 5 = 25 मीटर

एक चर वाले रैखिक समीकरण क्लास 8

प्रश्न 3.चीनी के मूल्य में 25 प्रतिशत की वृद्धि होने पर अब 1 किग्रा. चीनी का मूल्य 32 रु. है तो प्रारम्भ में चीनी का मूल्य प्रति किग्रा. क्या था?

हल:-
चीनी का वर्तमान मूल्य = 32
माना की पहले चीनी का मूल्य = 100
वर्तमान मू० = 32×100/125=3200/125 = 25.60

Bihar Board Class 8 Math Solution In Hindi Pdf Download

प्रश्न 4.दो विभिन्न मूल्यवाली 35 कलमों का कुल मूल्य 60 रु. है। यदि 1 सस्ती कलम का मूल्य 1.50 रु. एवं 1 महँगी कलम का मूल्य 2 रु. है तो कितनी महँगी कलमें खरीदी गईं?

हल:-
माना कि महंगी कलमों की संख्या = x
एवं सस्ती कलमों की संख्या = 35 – x
प्रश्नानुसार,
x +( 35 – x ) = 60
या 2 x X + 1.50 ( 35 – x ) = 60
या 2x + 52.5 – 1.50x = 60
या 2x – 1.50x = 60 – 52.5
या 0.5x = 7.5
या x = 7.5/0.5
x = 15
अतः महंगी कलमों की संख्या = 15

Bihar Board Class 8 Math Book Solution
प्रश्न 5.एक त्रिभुज के तीनों कोण 2 : 3 : 5 के अनुपात में है तो उनके तीनों कोण ज्ञात कीजिए।
हल:-
2 : 3 : 5
2x , 3x , 5x
माना कि पहला कोण = 2x
दूसरा कोण = 3x
तीसरा कोण = 5x
प्रश्नानुसार,
त्रिभुज के तीनों कोणों का योग = 180°
2x + 3x + 5x = 180°
या 10x = 180°
या x = 180°/10
x = 18°
अतः त्रिभुज का प्रथम कोण = 2x = 18 × 2 = 36°
त्रिभुज का दूसरा कोण = 3x = 18 × 3 = 54°
त्रिभुज का तीसरा कोण = 5x = 18 × 5 = 90°

Bihar Board Class 8th Math Solution प्रश्न 6.
बिल्लू के पास 1 रु. एवं 5 रु. के कुल 160 सिक्के हैं जिनका कुल मूल्य 310 रु. है। यदि 2 रु. के सिक्कों की संख्या 5 रु. के सिक्कों की संख्या की तिगुनी हो तथा 1 रु. के सिक्कों की संख्या = 40 है तो उसके पास प्रत्येक प्रकार के कितने सिक्के हैं?

हल:-
माना कि 5रु. के सिक्कों की सं० = x
एवं 2रु. के सिक्कों की सं० = 3x
एवं 1रु. के सिक्कों की सं० = 160 – x – 3x
= 160 – 4x
प्रश्नानुसार,
1 x ( 160 – 4x ) +2 x ( 3x ) + 5 x (x) = 300रु.
या 160 – 4x +6x + 5x = 300
या -4x + 6x +5x = 300 – 160
या – 4x + 11x = 300 – 160
या 7x = 140
या x = 140/7
x = 20
अतः
1 रु. के सिक्कों की सं० = 160 – 4 x 20
160 – 80 = 80
2 रु. के सिक्कों की सं० = 3 x 20 = 60
 5 रु. के सिक्कों की सं० = 20

bihar board class 8 math ganesh all classes

प्रश्न 7. पिता ने अपने तीन संतानों के बीच अपनी संपत्ति का बँटवारा 1 : 2 : 3 के अनुपात में करता है और अपने लिए 100000 रु. रखता है। यदि उसकी कुल संपत्ति 2.5 लाख रु. की हो तो प्रत्येक संतान को हिस्से के रूप में क्या मिला?

हल:–
माना कि पिता ने अपने पहली सन्तानो को सम्पति दी = xरु.
एवं पिता ने अपने दूसरी सन्तानो को सम्पति दी = 2xरु.
एवं पिता ने अपने तीसरी सन्तानो को सम्पति दी = 3xरु
प्रश्नानुसार,
x + 2x + 3x +100000 = 2,50000
या 6x = 2,50000 – 1,00000
या 6x = 1,50000
या x = 150000/6
x = 25000
अतः
पहली सन्तानो को सम्पति दी = 25000रु.
दूसरी सन्तानो को सम्पति दी = 2 x 25000 = 50,000रु.
तीसरी सन्तानो को सम्पति दी = 3 x 25000 = 75,000रु

bihar board class 8 math

प्रश्न 8. 11 के लगातार तीन गुणजों का योग 231 है तो उन्हें ज्ञात कीजिए।

हल:-
माना कि 11 का पहला गुणज = x
एवं 11 का दूसरा गुणज = x + 11
11 का तीसरा गुणज = x +22
प्रश्नानुसार,
x + ( x + 11 ) + ( x + 22 ) = 231
या x + x + 11 + x + 22 =231
या 3x + 33 = 231
या 3x = 231 – 33
या 3x = 198
या x = 198/3
x = 66
अतः
11 का पहला गुणज = 66
11 का दूसरा गुणज = 66 + 11 = 77
11 का तीसरा गुणज = 66 +22 =88

प्रश्न 9. संकुल संसाधन केन्द्र म.वि. फरना में आयोजित बाल मेले में प्रत्येक विजेता छात्र को 2 कलम एवं विजेता को छोड़कर शेष सभी प्रतिभागियों को 1 कलम दिया गया। यदि 100 छात्रों के बीच 120 कलम दिये गये तो विजेताओं की संख्या ज्ञात कीजिए।

माना कि विजेताओं छात्र की संख्या = x
विजेता छात्र को छोड़कर सभी प्रतिभागीयो की संख्या = 100 – x
प्रश्नानुसार,
2 x (x) + 1 (100-x) =120
या 2x + 100 – x = 120
या 2x – x = 120 -100
x = 20
अतः
विजेताओं छात्र की संख्या = 20

प्रश्न 10. रवि के पिता का वर्तमान उम्र रवि के वर्तमान उम्र के तिगुने से 5 वर्ष अधिक है। 5 वर्ष बाद उनके उम्रों का योग 47 वर्ष होगा। दोनों की वर्तमान उम्र ज्ञात कीजिए।

हल:-
माना कि रवि का वर्तमान उम्र = x वर्ष
एवं रवि के पिता का वर्तमान उम्र = 3x + 5 वर्ष
5 वर्ष बाद
रवि का उम्र = x + 5 वर्ष
रवि के पिता का उम्र = 3x + 5 + 5 = 3x +10 वर्ष
प्रश्नानुसार,
x + 5 + 3x + 10 =47
या 4x + 15 = 47
या 4x = 47 – 15
या 4x = 32
या x = 32/4
x = 8
अतः
रवि का वर्तमान उम्र = 8 वर्ष
रवि के पिता का वर्तमान उम्र = 3 x 8 + 5
24+5 = 29 वर्ष

bihar board class 8 math solution in hindi एक चर वाले रैखिक समीकरण Ex 2.3

निम्नलिखित समीकरणों का हल ज्ञात कीजिए –

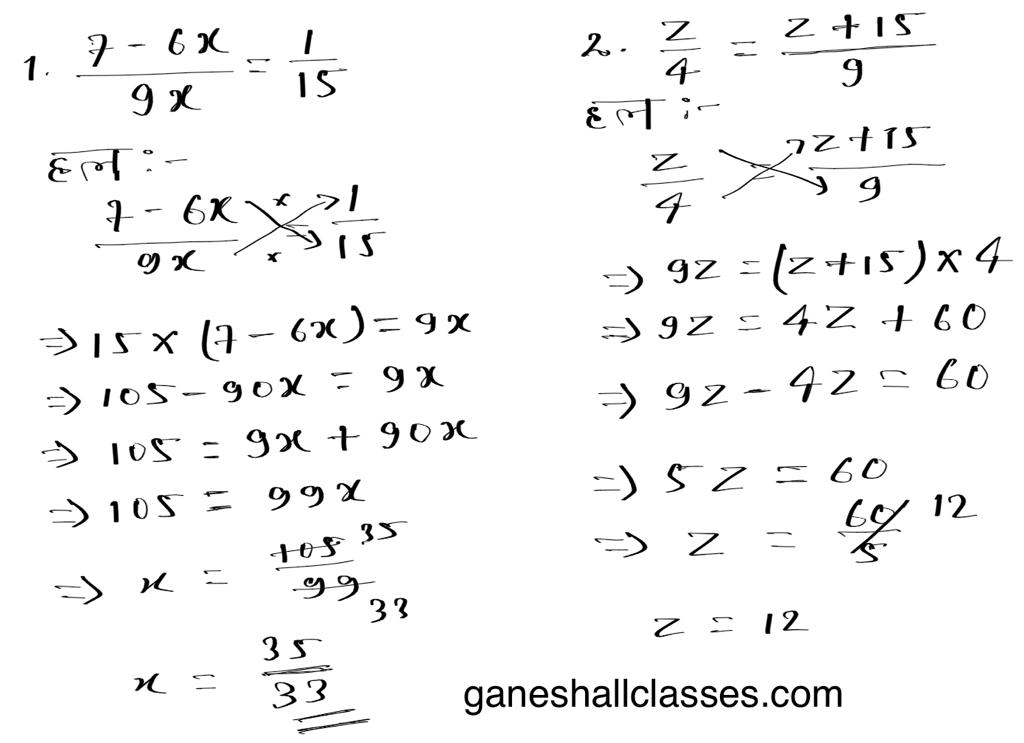
प्रश्न 3. x² – ( x- 2 )² = 32

हल:-
फार्मूला का प्रयोग करके -(a – b)² = a² – 2ab + b²
x² – ( x² – 2x.2 + (2)² ) = 32
या x² – ( x² – 4x + 4 ) = 32
या x² – x² + 4x – 4 = 32
या 4x – 4 = 32
या 4x = 32 + 4
या 4x = 36
या x = 36/4
x = 9

प्रश्न 4. (x + 4)² – (x – 5)² = 9

हल:-
सूत्र का प्रयोग करके –
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
( x² + 2.x.4 + 4² ) – ( x² – 2.x.5 + 5² ) = 9
या ( x² + 8x + 16 ) – ( x² – 10x + 25 ) = 9
या x² + 8x + 16 – x² + 10x – 25 = 9
या 8x + 10x +16 – 25 = 9
या 18x – 9 = 9
या 18x = 9 + 9
या 18x = 18
या x = 18/18
x = 1

प्रश्न 5. (y + 3) (y – 3) – y (y + 5) = 6

हल:-
सूत्र का प्रयोग करके –
( a + b) (a – b ) = a² – b²
y² – 3² – y ( y +5 ) = 6
या y² – 9 – y² -5y = 6
या -5y – 9 = 6
या -5y = 6 + 9
या -5y = 15
या y = -(15/5)
y = -3

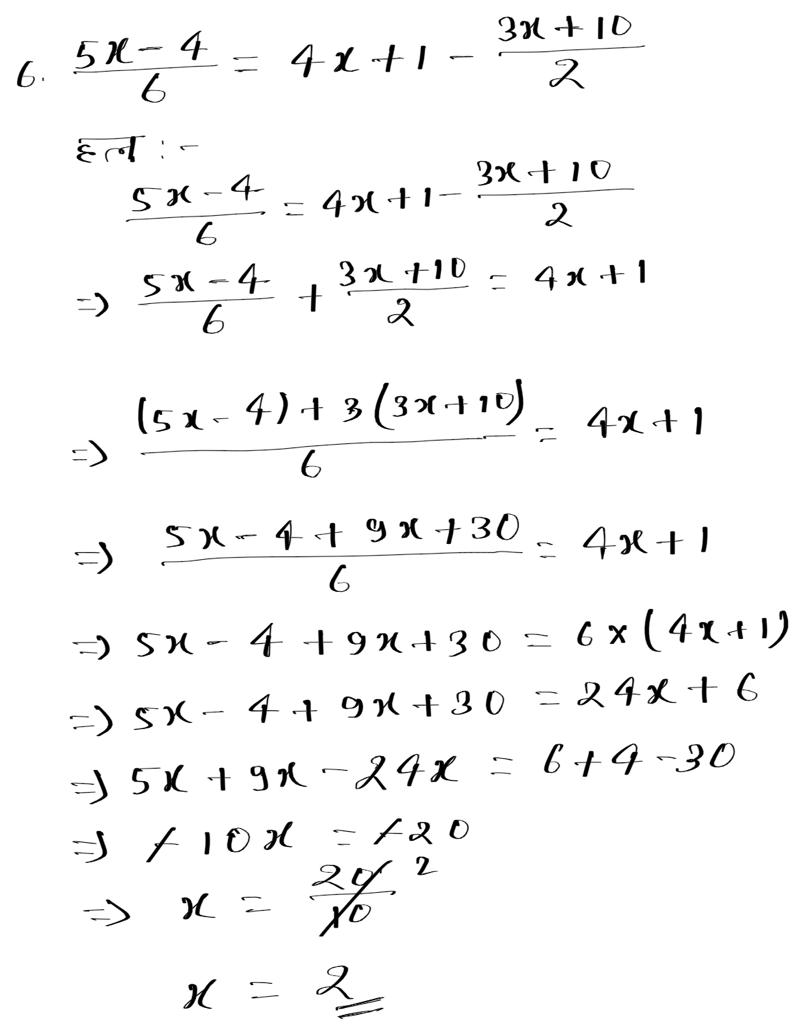
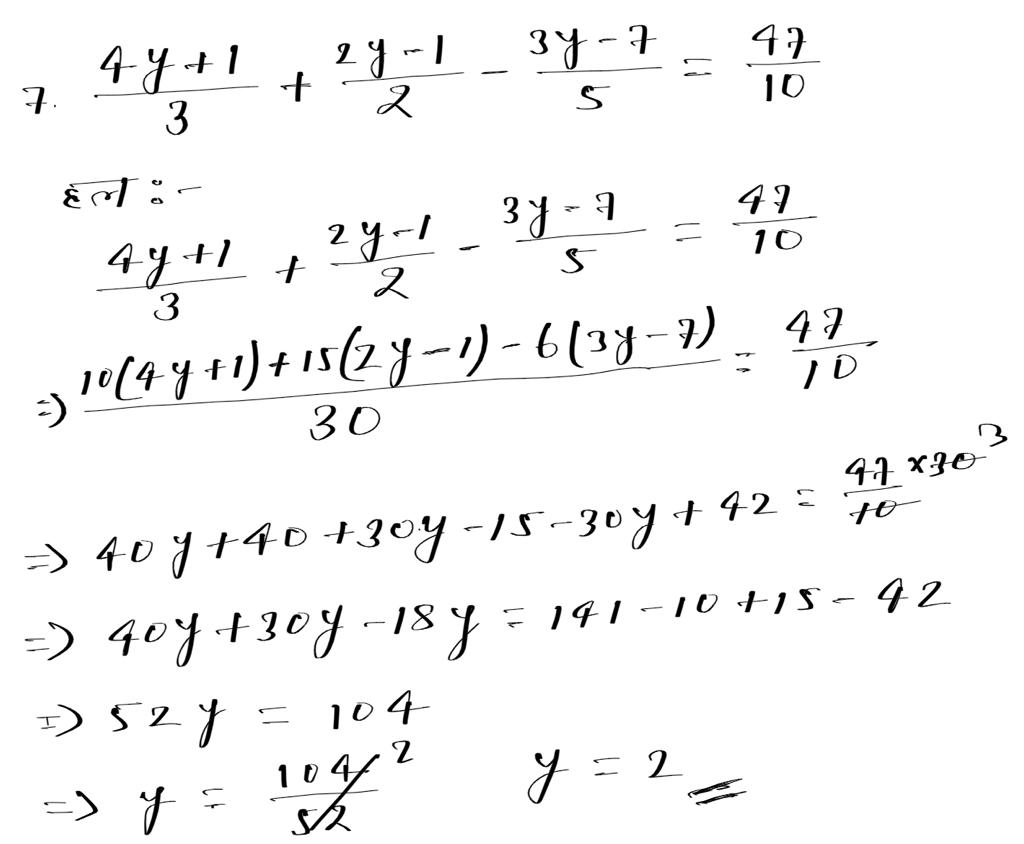
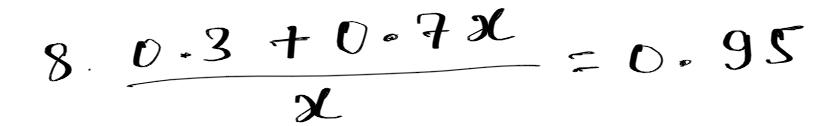
हल:-
0.3 + 0.7x = 0.95 x x
या 0.3 + 0.7x = 0.95x
या 0.3 = 0.95x – 0.7x
या 0.3 = 0.25x
या x = 0.30/0.25
x = 6/5
x = 1.2

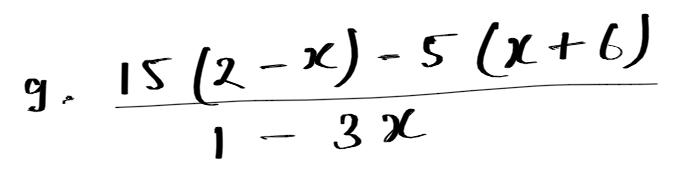
हल:-
15(2 – x) – 5(x + 6) = 6(1 – 3x)
30 – 15x – 5x – 30 = 6 – 18x
-20x = 6 – 18x
-20x + 18x = 6
-2x = 6
x = – (6/2)
x = -3

प्रश्न 10. दो अंकों की संख्या का दहाई अंक, इकाई अंक का तिगुना है। यदि अंक बदल दिये जाएँ तो प्राप्त संख्या मूल संख्या से 36 कम हो जाती है। वह संख्या ज्ञात कीजिए।

हल:-
माना कि इकाई अंक = x
एवं दहाई अंक = 3x
मूल संख्या = 10 x 3x + 1x = 31x
अंक बदलने पर
इकाई अंक = 3x
दहाई अंक = x
प्राप्त संख्या = 10x + 3x = 13x
प्रश्नानुसार,
31x – 13x = 36
या 18x = 36
या x = 36/18
x = 2
अतः मूल संख्या = 31 x 2 = 62

प्रश्न 11. एक नाव धारा की दिशा में एक घाट से दूसरे घाट तक जाने में 9 घंटे लगाती है । धारा की विपरीत दिशा में यही दूरी 10 घंटे में पूरा करती है। यदि धारा की चाल 1 किमी./प्रति घंटा हो तो शांत जल में नाव की चाल एवं दोनों घाटों के बीच की दूरी ज्ञात कीजिए।

हल:-
माना कि शांत जल नाव की चाल = x km/h
प्रश्न से,
धारा की चाल = 1 km/h.
धारा की दिशा में नाव की चाल = ( x + 1 )
दूरी / समय = चाल
दूरी / 9 घंटे = ( x + 1 )
दूरी = ( x + 1 ) x 9
दूरी = 9x + 9 —(i)
पुनः
विपरीत दिशा में नाव की चाल = ( x – 1 )
दूरी / समय = चाल
दूरी / 10 = ( x – 1 )
दूरी = ( x – 1 ) x 10
दूरी = 10x -10 —(ii)
समीकरण (i) एवं (ii) से
9x + 9 = 10x -10
या 9x – 10x = -10 – 9
या -x = -19
x1 = 19
अतः
शांत जल में नाव की चाल = 19 km/h.